Introducing GooseFX SSL v1: Single-Sided Liquidity with Less Slippage and More Protection

TL;DR

We introduce GooseFX SSL v1, a new design of AMM that: 1) enables simple single-sided liquidity provision, 2) enhances liquidity concentration and reduces slippage, and 3) protects LPs against impermanent loss. There are three key ingredients in our design. First, we dynamically adjust pool weights based on liquidity contribution. Secondly, we construct a curve that concentrates most of the liquidity around the current oracle price. Lastly, we do not allow traders to trade more favorably than the current oracle price.

1. The Problems

AMMs have been widely adopted throughout the crypto world since its inception back in 2016, based on its to its simplicity to do permissionless liquidity provision and be computationally efficient to be implemented on-chain. However, despite its widespread adoption, the AMM itself is not flawless. In this article, we discuss some of its problems and what are the efforts GooseFX SSL made toward fixing these problems.

There are three key problems in the current designs of automated market makers (AMM). First, liquidity provision is not user-friendly. When contributing liquidity, most AMMs require two or more tokens in an exactly specified ratio. For example, a constant-product market maker (CPMM, e.g. Uniswap v1/v2) requires liquidity providers to deposit a pair of tokens in a 50/50 ratio. In reality, the amount that users want to contribute is most likely not exactly equal to the required amount. Single-sided liquidity provision is the ideal form in terms of user experience yet. However, most AMMs do not allow this.

Secondly, liquidity is inefficiently scattered across all possible prices and, as a result, slippage is high. For example, for CPMM, liquidity is distributed evenly across the entire price space, which means that liquidity is wasted for the prices that are not touched. From the traders’ perspective, this also means constant slippage across the price space, even though slippage should ideally be small around some natural price (e.g. current price).

Lastly, liquidity providers are exposed to impermanent losses. Currently, most AMMs rely solely on arbitrageurs to anchor the pool price to the market price, but one major drawback of this automation is that any profits to the arbitrageurs are losses to the liquidity providers. In the setting of a constant-product market maker, when market price changes, LPs are guaranteed to trade in unfavorable terms, in order for pool price to adjust. There is growing consensus that liquidity providers’ interests need more protection. We want to limit losses to liquidity providers, especially when the market price can be accurately inferred.

We solve all three problems with GooseFX SSL v1.

2. GooseFX SSL v1, A New Design

We present a new AMM design that integrates single-sided liquidity pools with an innovative swap mechanism. In our design, each token corresponds to one single-sided liquidity pool. When a liquidity provider deposits one token into a pool (e.g. SOL), she gets back one g-token (e.g. gSOL), i.e. the LP token. When a trader wishes to demand liquidity, i.e. swap one token for another, he would interact with two pools at the same time. He must pay a transaction fee equal to his trading volume times a constant fee rate (currently at 0.40% but can be modified through governance). The fee accrues to the pool where he withdraws tokens, i.e. where he demands liquidity. We now describe the details of our design and how it achieves the desirable properties.

2.1 Dynamic Weights

To best illustrate our design, it is helpful to start with the well-known constant-product market maker (CPMM), e.g. Uniswap v1/v2. In CPMM, each pool consists of two tokens, with reserves x and y that are governed by the following equation:

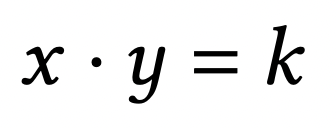
which can be expressed equivalently as the following differential equation:

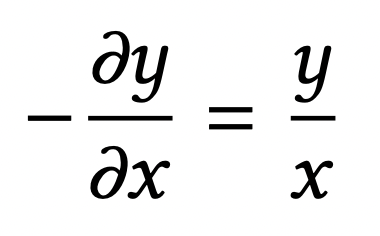
Our first departure from the simple CPMM is that we add dynamic pool weights:

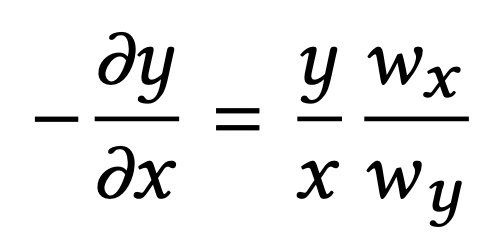
where w_x and w_y are pool weights determined by the amount of liquidity provided. As shown later in Section 3.1, dynamic weighting alone allows for single-sided liquidity provision without altering the pool price.

2.2 Oracle-Concentrated Swap Curve

Apart from the dynamic weights, our curve also contains an additional component that, as we show later in Section 3.2, has the property of concentrating liquidity around the current oracle price. Our final curve is as follows:

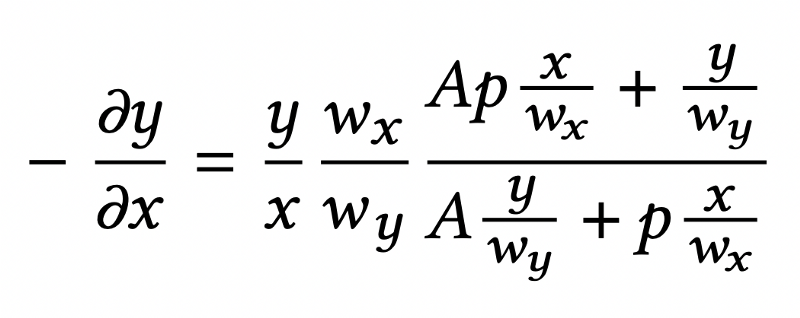
where p is the current oracle price and 𝐴 is a parameter that governs the shape of the curve.

The differential equation above gives the marginal price — that is, what is the price of x in terms of y when swapping an infinitesimal amount of x for y. To derive the amount of y to be received for any arbitrary amount of x, we solve the Initial Value Problem (IVP) of the differential equation.

2.3 Oracle-Tracking Swap Rule

On top of the curve above, we add a rule that, as we show later in Section 3.3, protects LPs from arbitrageurs. The rule is, in a nutshell, that swappers need to pay the worst of what our curve says and what the oracle says. For example, if the price derived by the curve is $100 for SOL/USDC, but the oracle currently says $110, we will sell SOL with the price of $110 to the trader instead of $100.

3. Single-Sided Liquidity with Less Slippage and More Protection

In this section, we illustrate why our AMM design achieves: 1) simple single-sided liquidity provision, 2) concentrated liquidity and low slippage, and 3) protection against arbitrageurs.

3.1 Single-Sided Liquidity Provision

How do we allow for single-side liquidity provision? The key is that our curve is not solely a function of the reserves but also of the pool weights that are dynamically adjusted. In CPMM, any deposits or withdrawals change pool reserves, which are the only inputs to determine pool prices. In contrast, in GooseFX SSL v1, deposits and withdrawals change both pool reserves and pool weights, which are adjusted so that pool prices remain invariant.

Mathematically, in CPMM, the pool price is simply y/x. Therefore, any deposits or withdrawals necessarily change pool prices, unless the amounts are in a very specific ratio (50/50 in value). In contrast, in GooseFX SSL v1, pool price is (y/w_y) / (x/w_x). Deposits and withdrawals change both the numerator and the denominator, and pool prices are kept unchanged, even if the deposits and withdrawals are in one token only.

3.2 Liquidity Concentration and Slippage

Our curve has the property of concentrating liquidity around the oracle price. Figure 1 shows swapping between a pair of tokens according to our curve (red lines), according to CPMM (black dashed line), and in a world with constant price (black solid line). We assume that the pool price is currently the same as the oracle price. The figure shows that, depending on the parameter 𝐴, GooseFX SSL price is near-constant for a large region around oracle price. In other words, there is very little slippage around the oracle price. In contrast, the CPMM price departs significantly from the oracle price even with small changes in reserves.

Figure 1: Swapping between two tokens

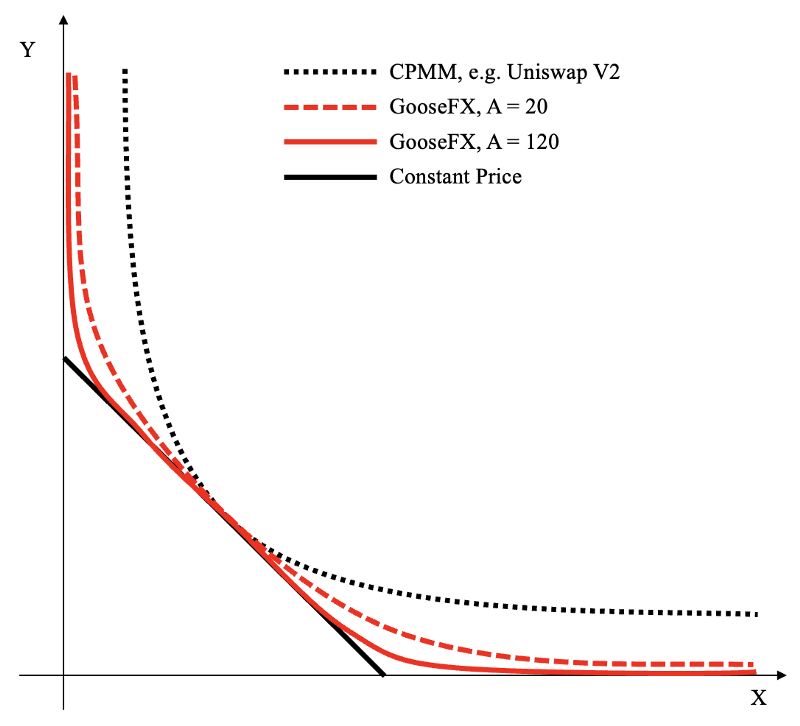
Figure 2 plots the distribution of liquidity across the price space, as defined in [4], which is basically the inverse of slippage:

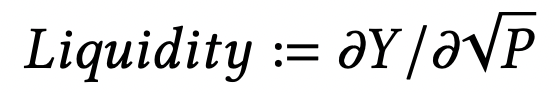
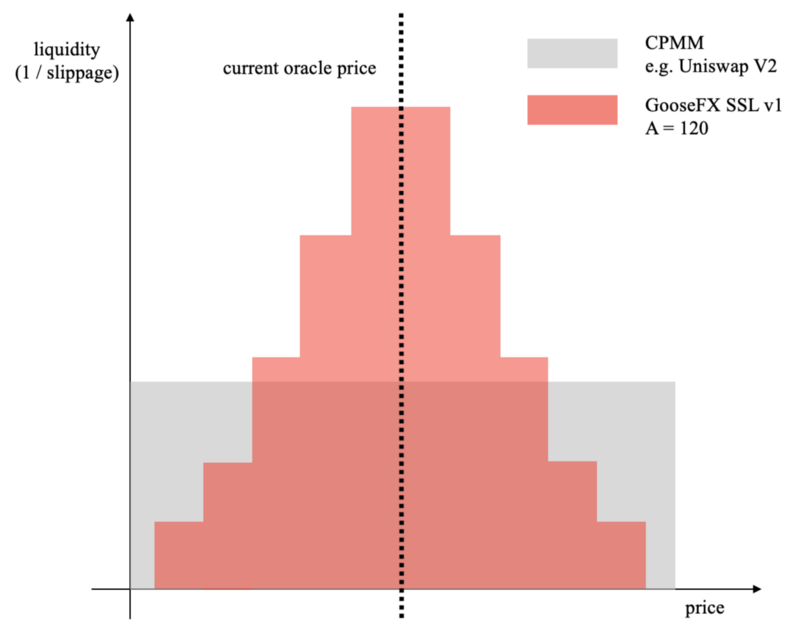
It shows that GooseFX SSL v1 concentrates liquidity around the oracle price whereas CPMM spreads liquidity evenly across all possible prices. In other words, slippage is much lower with GooseFX SSL v1, compared to CPMM.

Figure 2: Distribution of liquidity across price space

3.3 LP Protection against Impermanent Loss

By requiring agents to trade at the worst of the curve and the oracle, GooseFX SSL v1 provides LPs with effective protection against impermanent loss.

First of all, we eliminate any impermanent loss due to changes in oracle price. In a traditional AMM such as CPMM, when the oracle price changes, arbitrageurs would trade with the AMM at the outdated pool price and make a profit at the expense of LPs. As a concrete example, suppose that token 𝑡 ’s market price increases by 10%. Arbitrageurs can make a profit by buying from the pool and selling on the market, thereby draining the asset that has appreciated in value. In GooseFX SSL v1, arbitrageurs can never trade at a price better than the oracle price, and therefore LPs are protected from this type of impermanent loss.

What if arbitrageurs have private information on future prices? If we only use current oracle prices, then pool assets can be quickly depleted. For example, suppose that an informed trader knows that token x’s market price is going to increase by 10%. She would buy the token as much as possible as long as the price does not appreciate too much. That means if a pool strictly follows the oracle price then its token x would be quickly depleted by the trader (i.e. the black solid line crosses the x-axis and the y-axis). This is where our curve comes in as the savior. As the informed trader trades in one direction, the curve price adjusts and becomes the binding price. Therefore, in our design, LPs are (partially) protected from private information, where the amount of protection follows a tradeoff with liquidity concentration governed by parameter 𝐴.

4. Conclusion:

We introduce GooseFX SSL v1, which achieves three key functions missing partly or entirely in the current AMMs: 1) simple single-sided liquidity provision, 2) liquidity concentration and slippage, and 3) protection against arbitrage trades. In our next post, we will further demonstrate liquidity concentration, slippage, trading volume, and LP returns using simulation.

Website | Twitter | Telegram | Discord | Docs

Disclaimer: The statements, proposals, and details contained above are informational only, and subject to change. We are in early stage development and may need to change dates, details, or the project as a whole based on the protocol, team, legal or regulatory needs, or due to developments of Solana/Serum. Nothing above should be construed as financial or legal advice.